Batch 3 - Class 134 - Invariants 3

• In a special chess game played on 10x10 board, a "Camel" can do a 1,3 move i.e. move 1 square in any direction, and then 3 squares in a perpendicular direction. Is it possible for the camel to move to an adjacent square through a sequence of moves?
• Answer: No. The camel always remains on the same colored square

• A statement that does not change from one step to another in a problem
• Must be relevant to solving the problem (for example, "Sum of first five whole numbers is 15" is an invariant for all problems, but it doesn't help solve any problem)
• Is not a constant (for example, "the number of birds" in the sparrow/tree problem - again doesn't help solve the problem)
• Note that fitting an invariant doesn't guarantee a solution in many cases. Not fitting one can guarantee lack of a solution. (Again, think about irrelevant invariants)
• Parity is a special case of invariance
• Revision Exercise:
• 8x8 table with all squares white except one. Can you toggle rows and columns successively to get all white
• 3x3 table with one of the corners black
• 8x8 problem with four corners black

  Note that in all of the above, we realized that as long as there is a even sub-grid with odd blacks, toggling can't create an all-white, because odd-parity of blacks is an invariant

• Coloring is another case of invariance
• Can you cover a 8x8 chessboard with fifteen 1x4 and one L-polymino? 

• Answer: No. Color alternate rows of chessboard black and white. The 1x4 polynimos occupy even number of whites each regardless of how you place it. The last one occupies odd number of whites. Total number of whites to be covered is even.
• Can you cover 10x10 board using polynimos shown below?

• Answer: No - works with standard coloring of chessboard!
• Prove that a 102x102 board cannot be covered using 1x4 polynimos
• Answers

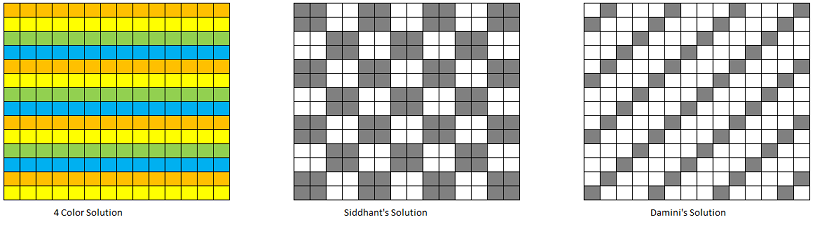
• 4 Color Solution: Color each row by colors 1,2,3,4 alternately. Each polynimo either covers a color completely (4 squares), or covers any two colors once. So the difference in uncolored cells of any two colors changes by 4 or 0 at each step. Since color 1 has 102x26 squares and color 3 has 102x25 squares, the difference is 102, which is not divisible by 4. Hence those two colors will never get to 0 simultaneously.
• Siddhant's Solution: Color the board into blocks of 2x2 as shown. Each polynimo will cover exactly 2 whites and 2 black squares. However, there are 4 more black squares than white, and hence the board can't be covered just using 1x4 polynimos.
• Damini's Solution: Color the board along diagonals as shown. Each polynimo will cover an odd number of white and black squares. The total number of polynimos required (51 x 51) are odd. Hence these polynimos can not cover an even number of black and white squares on the grid.

• Prince Ivan is trying to kill a monster with 20 heads. The prince has two swords, one which can cut 7 heads, and another which can cut 4 heads but 25 heads grow back when you do that. Can the prince severe all heads of the monster. Note that none of the swords can cut off less or more heads than they are made for.
• Answer: No, because number of heads each sword can cut does not change the remainder modulo 7, whereas 20 is not divisible by 20.
• Idea of Remainder as an invariant - Parity is just remainder modulo 2
• Dr Gizmo has invented a machine which takes a coin and gives 5 coins of same aggregate value as the initial coin. Show that starting with one coin, you can not land up with 26 coins.
• Answer: Remainder modulo 4 is an invariant
• There is a heap with 1001 stones on the table. At each step, you take a heap with more than one stone, throw one stone away, and divide the rest into two heaps. Can you get to a stage where all heaps on the table have 3 stones each?
• Answer: No. The invariant is number of stones + number of heaps. With k heaps of 3 stones, this value would be 3k+k=4K. Since 1002 is not divisible by 4, this is not possible

• There are three printing machines. One takes a card (a,b) and returns a card (a+1,b+1). The second takes a card with even numbers on it and returns (a/2,b/2). The third takes two cards (a,b) and (b,c), and returns (a,c). Each machine also returns back the initial cards. Starting from (5,19), can you get to (1,1988)
• Work through steps with kids

  In first machine, what could be the invariant? Difference of the two numbers. In the second, the difference gets halved. In the third, the differences get added. So the difference is not the invariant, but the invariant may have to do something with the difference

  Now lets observe for few steps

  (5,19) -> (6,20)(6,20) -> (3,10)(3,10) -> (4,11) ... -> (20,27)(6, 20) and (20,27) -> (6,27)What are the differences - 14, 14, 7, 7, 21 - All divisible by 7! Can we now prove the invariant?
• Since 1988-1 is not divisible by 7, we can't get that card